Quine – Mc Cluskey method of minimization:

 Quine – Mc Cluskey method of minimization:

Quine – Mc Cluskey method uses tabular column to minimize the expression. It is similar to Karnaugh Map. But in Quine – Mc Cluskey method Boolean functions with more variables can be solved. 

This method was first developed by William V. Quine in 1952 and it was further extended by Edward J. Mc Cluskey in 1956. Hence this method is named after them as Quine – Mc Cluskey method. It is also called as method of prime implicants.

Steps to be followed to minimize using Quine – Mc Cluskey method:

Step 1:

The Boolean function has to be written in Minterm. If not written, the individual Minterm have to be found. Then it should be converted into equivalent binary numbers.

Step 2:

Next step is to form a tabular column. The binary numbers should be grouped according to the number of 1’s in them. The binary number with one 1’s are grouped into one set. The binary number with two 1’s are grouped into one set. This is continued till all the binary numbers are grouped.

Step 3:

In each group find the binary numbers which differ by only one bit and put a tick mark near the number. Form a new tabular column and put dash ‘-’ in the place where the paired binary numbers differ by one bit.

Step 4:

Next the binary numbers are compared with the other groups and find the numbers which differ by one bit. Form another tabular column and write the binary numbers and put dash ‘-’, in the place where the numbers differ by 1 bit.

Step 5:

Continue this till all the binary numbers are paired and written. If any binary number is left without grouping and pairing.

Step 6:

Prime implicants table is plotted. ‘ x’ is marked across each essential prime implicants. Tick mark is put against every column which has only one cross mark. The final minimized expression is written from this prime implicants table.

Example 1:

Solve the following Boolean expression using Quine – Mc Cluskey method.

F(A,B,C,D)=∑m(1,2,3,7,8,9,10,11,14,15)

Solution :

Step 1:

Write the binary numbers for all the Minterm:

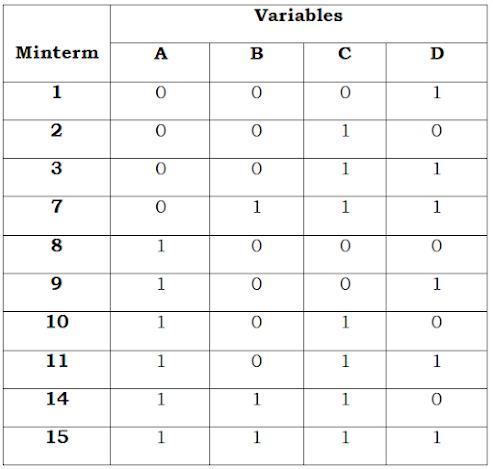Binary numbers for the minterm

Step 2:

Grouping the minterm according to the number of 1’s present in it.

Grouping Minterms

Step 3:

Look for the binary numbers which differ by one bit and combine. Form a tabular column for 2 cell combinations. Put a dash ‘-’ where it differs by 1 bit.

Combining binary numbers which differ by 1 bit

Step 4:

Again combine 4 cells which differ by one bit from the above tabular column and form a new tabular column. ‘-’ is also considered as a bit.

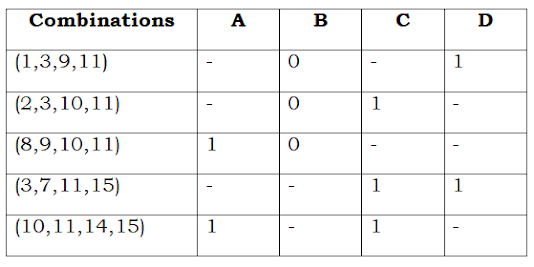Combining 4 cells which differ by 1 bit

Step 5:

Prime implicants table is plotted. ‘x’ is marked across each essential prime implicants. Tick mark is put against every column which has only one cross mark.

Prime implicant table

Consider the prime implicants with tick mark and write the minterm referring the previous tabular column to get the final minimized solution.

F(A,B,C,D)=B'D+B'C+AB'+CD+AC