NAND–NOR implementations:
Any Boolean expression can be implemented by NAND-NOR gates. For this, first the expression should be converted into SOP or POS form. NAND and NOR gates are called as universal gates and the Boolean expression can be implemented without the use of any other gates.
Any logic circuit is converted into NAND- NOR circuit because they are widely used commercially because of its wired logic. Wired logic means NOR gate is not physically used but using just wires this logic can be obtained.
NAND-NOR implementation reduces the number of gates and reduces the size of the circuit. This in turn reduces the implementation cost and the power consumption. Another reason is the fabrication process of NAND and NOR gate is very easy and it is of low cost.
Implementing NOT, OR, AND into NAND gate:
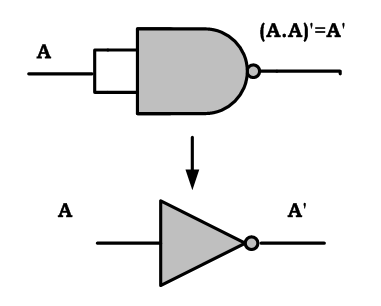
Implementing NOT gate using NAND gate:
(A.A)'=A' (Idempotent Law)
Implementing NOT Gate using NAND Gate
Implementing AND gate using NAND gate:
((AB)' (AB)')'= ((AB)')' (By Idempotent Law)
= AB (Involution Law)
Implementing AND Gate using NAND Gate
Implementing OR gate using NAND gate:
((AA)'(BB)')'= (A'B')' (By Idempotent Law)
= A''+B'' (By De Morgan’s Law)
= A+B ( By involution Law)
 |
| Implementing OR Gate using NAND Gate |
Implementing NOT, OR, AND into NOR gate:
Implementing NOT gate using NOR gate:
(A+A)'=A' (By Idempotent Law)
 |
| Implementation of NOT Gate using NOR Gate |
Implementing OR gate using NOR gate:
((A+A)'+(B+B)')'= (A'+B')' (By Idempotent Law)
= A''.B'' (By De Morgan’s Law)
= A.B ( By involution Law)
 |
| Implementing OR Gate using NOR Gate |
Implementing AND gate using NOR gate:
((A+A)'(B+B)')'= (A'+B')' (By Idempotent Law)
= A''.B'' (By De Morgan’s Law)
= A.B ( By involution Law)
Implementing AND Gate using NOR Gate
Equivalent Gates:
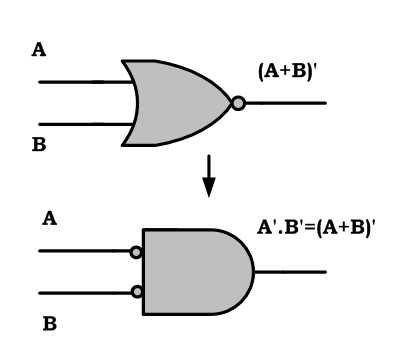
1) NAND gate is equivalent to the inverted input OR gate:
 |
| NAND gate is equivalent to the inverted input OR gate |
2) AND gate is equivalent to the inverted input NOR gate:
AND gate is equivalent to the inverted
input NOR gate:
3) NOR gate is equivalent to the inverted input AND gate:
NOR gate is equivalent to the inverted
input AND gate:
4) OR gate is equivalent to the inverted input NAND gate:
OR gate is equivalent to the inverted
input NAND gate:
Example 1:
Implement the following SOP expression using NAND gates:
Y=ABC+BCD+CDE
Step 1:
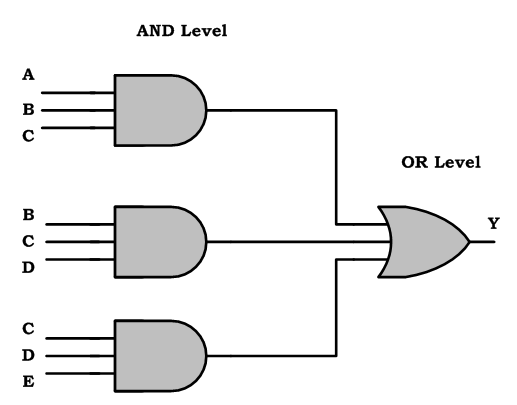 |
| Implementing SOP expression using AND, OR Gates |
Step 2:
Bubbles are introduced at the output of the AND gate and at the input of the OR gate.
Bubbles at the input and output
Step 3:
Bubbled input OR gate is replaced with NAND gate. Now all the gates are NAND gate.
All gates replaced by NAND gate
Example 2:
Implement the following POS expression using NOR gates:
Y=(A+B+C).(B+C+D).(C+D+E)
Step 1:
 |
| Implementation POS expression using OR, AND gate |
Step 2:
Bubbles are introduced at the output of the OR gate and at the input of the AND gate.
Bubbles introduced in the input and output
Step 3:
Bubbled input AND gate is replaced with NOR gate. Now all the gates are NOR gate.
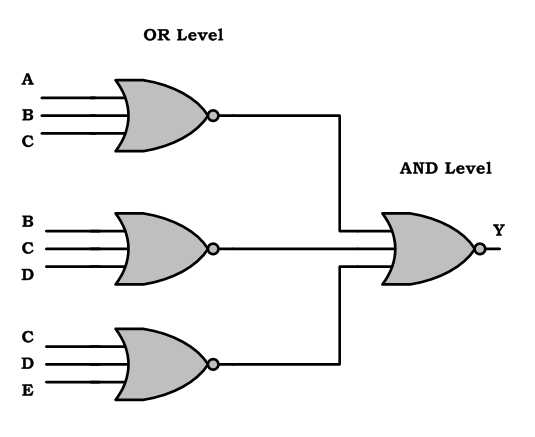 |
| All gates replaced by NOR Gate |









0 Comments