Minterm and Maxterm, Examples for Minterm and Maxterm

 Minterm and Maxterm

Boolean function can be put in two ways. They are 

1. Canonical Minterm and 

2. Canonical Maxterm.

Minterm:

Minterm is a product term in which the Boolean variable is either normal or in complemented form.

Let us consider the below truth table and write the Boolean Minterm expression.

Truth table for Minterm

Steps to write the Boolean Minterm expression:

Step 1:

A,B,C are the inputs and F is the output. To write the Minterm consider the rows which has the output F=1. In the above truth table m1, m3, m5, m7 have  outputs ‘1’. The input which has the value ‘1’ is written as such and the input which has the value ‘0’ is complimented. 

For example in the row 1, the output F=1 and the inputs A=B=0. So the inputs A and B are complimented and C is written as such. So the Minterm is A'B'C. 

Step 2:

The Minterm f can be written as the sum of all the products of the row which has the output 1.

   f= A'B'C+ A'BC+ AB'C+ ABC

It can also be represented as 

f(A,B,C)= m1+ m3+ m5+ m7

Or it can be written as

f(A,B,C)= ∑m(1,3,5,7)

Maxterm:

Maxterm is a sum term in which the Boolean variable is either normal or in complemented form.

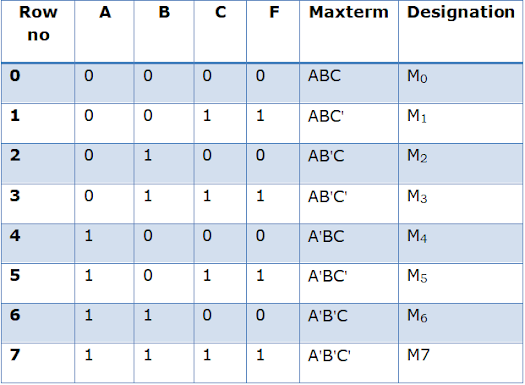Truth table for Maxterm

Steps to write the Boolean Maxterm expression:

Step 1:

A,B,C are the inputs and F is the output. To write the maxterm consider the rows which has the output F=0. In the above truth table M0, M2, M4, M6 have outputs ‘0’. The input which has the value ‘0’ is written as such and the input which has the value ‘1’ is complimented. 

For example in the row 2, the output F=0 and the inputs A=C=0 and B=1. So the input B is complimented and A and C are written as such. So the maxterm is AB'C. 

Step 2:

Considering all the rows which has the output ‘0’ the Maxterm can be written as

f= (A+B+C).(A+B'+C).(A'+B+C).(A'+B'+C)

It can also be written as

f(A,B,C)= M0+M2+M4+M6 

Or f(A,B,C)=πM (0,2,4,6)

Examples for Minterm and Maxterm:

Problem 1:

Express the Boolean function F=A+BC as minterm

F= A(B+B')(C+C')+BC(A+A')      

  

By complement law A+A'=1. Adding all the input variables in the product terms we get

F=(AB+AB')(C+C')+ ABC+ A'BC

F= ABC+ABC'+AB'C+ABC'+AB'C'+ABC+A'BC

There are two ABCs and ABC'. So let us consider one ABC and ABC'

F= ABC+ ABC'+AB'C+ AB'C'+ A'BC

In minterm the ‘1’ input is written as such and the input ‘0’ is complimented.

F= 111+110+101+100+011

F= m7+m6+m5+m4+m3

F=∑m(3,4,5,6,7)

Problem 2:

Express the Boolean function F=A+BC as Maxterms

F=A+(BC)

After removing the bracket and expanding we get

F= (A+B).(A+C)

By complement law CC'=BB'=1. So after adding all input terms in the expression we get,

F= (A+B+CC').(A+C+BB')

F= (A+B+C).(A+B+C').(A+C+B).(A+C+B') 

There are two (A+B+C)s. So let us consider one (A+B+C)

F= (A+B+C).(A+B+C').( A+B'+C)

In Maxterm the input ‘0’ is written as such and the input ‘1’ is complemented.

F=(0+0+0).(0+0+1).(0+1+0)

F= M0.M1.M2

F= πM(0,1,2)