Karnaugh Map
We have already discussed
about minimizing the Boolean expressions using Boolean algebra, postulates and
theorems. They are all time consuming. To make the process very simple and easy
K map is used.
What is Karnaugh Map (K Map)?
Karnaugh Map is used to minimize the Boolean expressions without using Boolean algebra and theorems. It is a tool used to represent the Boolean function.
It is a table with rows and
columns. It is filled with 0’s or 1’s. Both sum of products (SOP) and product
of sums(POS) are represented by K map. It has 2n cells for n
variables.
Steps to solve the
expression using K map:
1.First
select number of cells. For n variables 2n cells are required.
Example: 2 variable expression, the number of cells
will be 22. So the number of cells is 4. For 3 variables the number
of cells is 8. For 4 variables the number of cells required will be 16.
 |
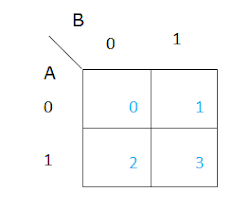
| Cell construction of k map |
 |
| Numbering of 4 cells in the K map |
 |
| Numbering of 8 cells in K map |
 |
| Numbering of 16 cells in K map |
 |
| Truth table |
 |
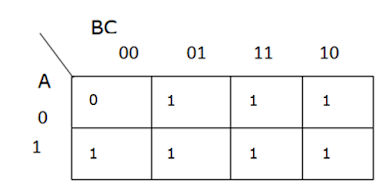| Entering the values in the K map |
So here the input A is in one axis and BC is in another axis. Respective output D is entered in the cells.
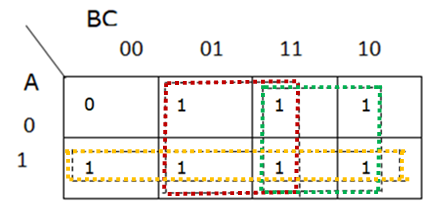
4. After transferring the values from truth table to k map, the adjacent cells are grouped. In SOP the cells with the value ‘1’ are grouped. In POS the cells with the value ‘0’ are grouped.
It is grouped into groups of 2, 4 and 8. While grouping overlapping and wrap around are allowed. Cells should not be grouped diagonally.
 |
| Grouping of K map |
5.Now identify the common variables within each loop and form a SOP expression by summing up together.
 |
| Identifying common variable in the loops |
In
the red group C is common. In the green group B is common in the orange group A
is common. So the SOP expression will be
D=
C+B+A
0 Comments