De Morgan’s theorem, De Morgan’s theorem 1, De Morgan’s theorem 2:

 De Morgan’s theorem:

Augustus De Morgan is a British mathematician, who lived in 19th century. He formulated two important theorems of Boolean algebra.

Demorgan’s law is all about breaking long bars into small individual bars. If you break the long bar over the addition, it will be splitted into individual multiplication. In the same way if you break a long bar over the multiplication, it will be splitted into individual addition bars.

De Morgan’s theorem 1:

The compliment product of two variables is equal to the sum of compliment of each variable.

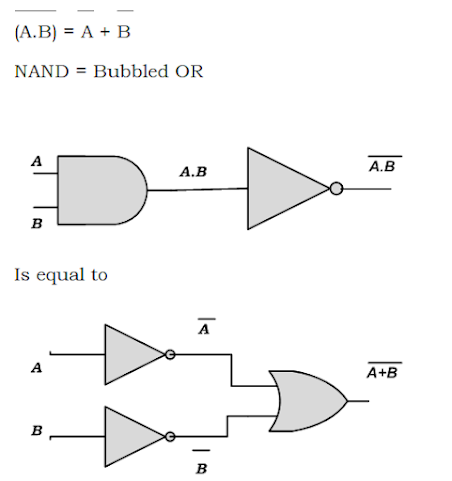De Morgan's first theorem

Here A and B are two variables. The L.H.S is the compliment of the AND gate. In R.H.S the complimented A and B variable is given as input to the OR gate.

Verification of De Morgan's first theorem using truth table:

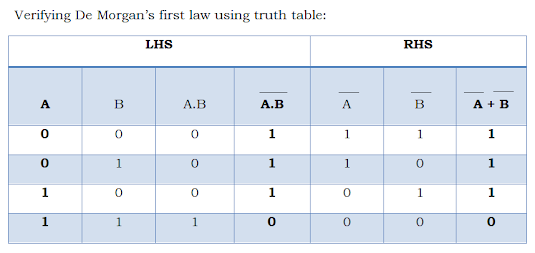Verification of first theorem

De Morgan’s theorem 2:

The compliment of the sum of two variables is equal to the product of the compliment of each variable.

De Morgan's 2nd theorem

Here in LHS the output of the OR gate is complimented. In RHS the A and B variables are inverted and given as input to the AND gate.

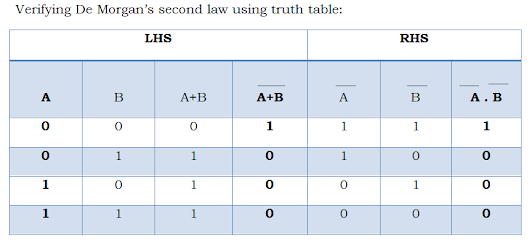Verification of 2nd theorem

De Morgan’s theorem for three input variables:

A, B and C are the three input variables. The compliment of the product of all the three variables is equal to the sum of compliment of each variable.

The compliment of the addition of the three variables is equal to the product of the compliment of each variable. This continues and keeps going on.